Rekurzia v programovaní je, ak procedúra volá samu seba. Aby rekurzia pracovala korektne, parametre, ktoré používa, by mali po nejakom čase dôjsť do stavu, v ktorom sa rekurzia zastaví.
Rekurzia môže byť priama, keď procedúra volá samu seba priamo a môže byť nepriama, ak procedúra vyvolá inú procedúru a táto vyvolá pôvodnú procedúru.
Pomocou rekurzie možno naprogramovať mnohé úlohy výrazne jednoduchšie než bez nej.
Na hodine sme naprogramovali funkciu faktoriál. Faktoriál prirodzeného čísla ![]() je súčin všetkých prirodzených čísel od 1 po n. Faktoriál čísla
je súčin všetkých prirodzených čísel od 1 po n. Faktoriál čísla ![]() označujeme
označujeme ![]() .
.
Keď si napíšeme faktoriály prvých piatich prirodzených čísel dostaneme:
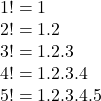
Keď sa na to pozorne pozrieme, zistíme, že pre ![]() . Z toho vyplýva, že faktoriál by sme mohli naprogramovať pomocou rekurzie.
. Z toho vyplýva, že faktoriál by sme mohli naprogramovať pomocou rekurzie.
Nasledujúca procedúra vypočíta faktoriál:
viem faktorial :n
ak2 :n=1
[vysledok 1]
[vysledok :n*faktorial(:n-1)]
koniec
Poznámka: vysledok je hodnota, ktorú vráti procedúra procedúre, ktorá ju vyvolala.
Keď sme do príkazového riadka napísali
pís faktorial 5
Imagine vypísal 120. Keď sme číslo postupne zväčšovali, pre pis faktorial 13 imagine vypísal 6.22702E9. Veľmi veľké čísla program vypísuje v takzvanej vedeckej notácii. Znaky E9 znamenajú, že 6.22702 máme vynásobiť číslom ![]() , čo zodpovedá jednej miliarde.
, čo zodpovedá jednej miliarde.
Keď sme vstupný parameter ďalej zväčšovali, pre pis faktorial 21 sme dostali 5.10909E19 pre parameter 22 imagine vypísal Chyba v procedúre faktorial: Pri vykonávaní * nastala chyba v reálnej aritmetike
Poznámka k reprezentácii čísel v počítačoch, doplnkové učivo
Číslo, ktoré malo byť výstupom procedúry faktoriál, bolo pre imagine príliš veľké a imagine s takými veľkými číslami nevie pracovať. Každý programovací jazyk má pre jednotlivé číselné typy vyhradenú nejakú pamäť. Napríklad pamäť jeden bajt (angl. byte), môže reprezentovať prirodzené čísla 0 až 255 alebo celé čísla -128 až 127. Pamäť dvoch bajtov môže reprezentovať prirodzené čísla 0 až 65535 alebo celé čísla -32768 až 32767, pamäť 4 bajty môže reprezentovať prirodzené čísla 4294967295 (imagine nám to už prevedie do vedeckej notácie) alebo celé čísla -2147483648 až 2147483647. Reprezentácia reálnych čísel je komplikovanejšia. Časť vyčlenenej pamäte je vyhradená na platné číslice a druhá časť na mocninu desiatky. Kým s celými číslami pracujú počítače presne (pokiaľ nedôjde k prekročeniu rozsahu), reálne čísla môžu byť zaokrúhlené. Je to nastavené tak, aby relatívna chyba bola čo najmenšia. Ešte to zvykne byť urobené tak, že počítač vnútorne pracuje s väčšou presnosťou, než nám zobrazí na výstupe. Vnútorne si pamätá o dve až tri platné číslice viac než zobrazí. Preto väčšinou neprídeme nato, že sa v skutočnosti dopúšťa nejakej nepresnosti. Pri neopatrnom narábaní s reálnymi číslami táto nepresnosť môže nadobudnúť veľké hodnoty. Podrobnejšie sa s počítaním s reálnymi číslami v počítačoch alebo v kalkulačkách oboznámite na strednej škole.
Faktoriál bez rekurzie
Na porovnanie uvádzam výpočet faktoriálu bez použitia rekurzie. Je vecou vkusu, ktorý z týchto spôsobov výpočtu budete pokladať za programátorsky elegantnejší, obe majú päť riadkov, v tejto procedúre máme o jednu premennú navyše. Rekurzívne volanie na druhej strane spotrebúva pamäť, systém si musí pamätať cestu po ktorej sa vráti na miesto odkiaľ bola procedúra volaná. Ak sa rekurzia včas nezastaví, môže dôjsť k vyčerpaniu pamäte počítača. Rekurzívne riešenie tiež môže niekedy dlhšie trvať než nerekurzívne.
viem faktorialbezrekurzie :n
urob „f 1
opakuj :n-1 [urob „f :f*:n urob „n :n-1]
vysledok :f
koniec
Kochova vločka
V ďalšej časti hodiny sme naprogramovali Kochovu krivku. Švédsky matematik Helge von Koch v roku 1904 publikoval prácu o krivke, ktorá vznikne nasledujúcim postupom:
- Nakreslíme úsečku:

- Úsečku rozdelíme na tretiny a nad bodmi prvej a druhej tretiny zostrojíme rovnostranný trojuholník, úsečku medzi vrcholmi, ktoré ležia na pôvodnej úsečke zmažeme. Vznikne nasledujúci útvar:

- To isté zopakujeme pre každú úsečku hore uvedeného útvaru. Dostaneme:

- To isté robíme s novým a novým útvarom do nekonečna. Po 8 krokoch dostaneme:

Kochova krivka bola objavená ako jedna z prvých fraktálnych kriviek. Pozri fraktál.
Vyššie uvedené útvary môžeme nakresliť nasledujúcou procedúrou:
viem koch :dlzka :uroven
ak2 :uroven=0
[dopredu :dlzka]
[
koch (:dlzka/3) (:uroven-1)
vlavo 60
koch (:dlzka/3) (:uroven-1)
vpravo 120
koch (:dlzka/3) (:uroven-1)
vlavo 60
koch (:dlzka/3) (:uroven-1)
]
koniec
Pokiaľ by sme to isté robili nie nad úsečkou, ale nad pravidelným mnohouholníkom, dostaneme Kochove vločky. Kochove vločky nakreslíme napríklad takto:
viem hviezda :dlzka :uroven
znova
ph
dopredu 100
pd
vpravo 90
opakuj :uroven+2
[
koch :dlzka :uroven
vpravo 360/(:uroven+2)
]
koniec
Postupne dostaneme nasledujúce vločky:




Naprogramovanie Kochovej krivky bez použitia rekurzie by bolo veľmi ťažkopádne, ak nie nemožné. Použil by sa príkaz opakuj.
One Comment